![]() である。これを踏まえて、
である。これを踏まえて、![]() を既約分数で表せ
を既約分数で表せ
![]() とおき、1000000倍して小数部を取る。
とおき、1000000倍して小数部を取る。
![]()
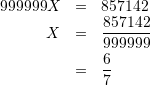
これは、解き方を知っていたのでできたのだが、約分するのに電卓使ったので反則か?解答はもっとクールだった。というか、この解法では全然「これを踏まえて」ないのでダメですね。約分も難しい(電卓使いました)し。
模範解答は、![]() としておいて、
としておいて、
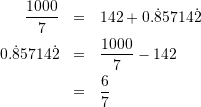
しかし、約分するときが気がついたんだけど、![]() 、面白いな。
、面白いな。
![]() である。これを踏まえて、
である。これを踏まえて、![]() を既約分数で表せ
を既約分数で表せ
![]() とおき、1000000倍して小数部を取る。
とおき、1000000倍して小数部を取る。
![]()
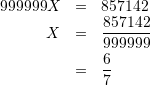
これは、解き方を知っていたのでできたのだが、約分するのに電卓使ったので反則か?解答はもっとクールだった。というか、この解法では全然「これを踏まえて」ないのでダメですね。約分も難しい(電卓使いました)し。
模範解答は、![]() としておいて、
としておいて、
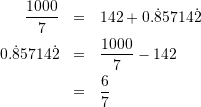
しかし、約分するときが気がついたんだけど、![]() 、面白いな。
、面白いな。