2桁の2進数![]() を表す整数を
を表す整数を![]() とする。2進数
とする。2進数![]() が表す整数を
が表す整数を![]() の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
- ア

- イ

- ウ

- エ

2進数![]() を表す整数
を表す整数![]() は、
は、
(1) ![]()
2進数![]() を表す整数
を表す整数![]() は、(1)同様
は、(1)同様
(2) ![]()
(1)を![]() と変形して(2)に代入すると
と変形して(2)に代入すると
(3) 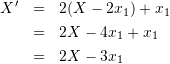
ここで、![]() を2で割った商は、
を2で割った商は、
(4) 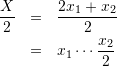
![]() となる。したがって、
となる。したがって、
(5) ![]()
(5)を(3)に代入して、![]() よって答えウ
よって答えウ
2桁の2進数![]() を表す整数を
を表す整数を![]() とする。2進数
とする。2進数![]() が表す整数を
が表す整数を![]() の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
2進数![]() を表す整数
を表す整数![]() は、
は、
(1) ![]()
2進数![]() を表す整数
を表す整数![]() は、(1)同様
は、(1)同様
(2) ![]()
(1)を![]() と変形して(2)に代入すると
と変形して(2)に代入すると
(3) 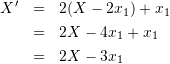
ここで、![]() を2で割った商は、
を2で割った商は、
(4) 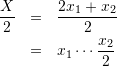
![]() となる。したがって、
となる。したがって、
(5) ![]()
(5)を(3)に代入して、![]() よって答えウ
よって答えウ