その理屈、証明できますか
予想2 ![]() が1より大きな整数で、かつ
が1より大きな整数で、かつ![]() が素数でなければ
が素数でなければ![]() は素数でない
は素数でない
![]() は素数ではないので、
は素数ではないので、![]() かつ
かつ ![]() となる2つの正の整数
となる2つの正の整数![]() が存在する。
が存在する。![]() とする。そのとき次のとおり。
とする。そのとき次のとおり。
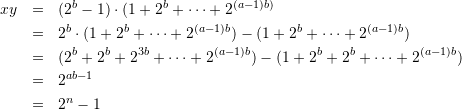
下の展開式はいいとしても、そもそも![]() の式の立て方というか突如出現したかに見えるこの式の存在。これが僕のような凡人には理解できないところ。この式がなぜ・どういう思考回路を経て出現したのか?そこがわからないと「証明は難しい」のまま終わってしまう。そのあたりは後々の章であきらかになるのかな?とりあえず、期待して読み進む。
の式の立て方というか突如出現したかに見えるこの式の存在。これが僕のような凡人には理解できないところ。この式がなぜ・どういう思考回路を経て出現したのか?そこがわからないと「証明は難しい」のまま終わってしまう。そのあたりは後々の章であきらかになるのかな?とりあえず、期待して読み進む。
