純粋関数型データ構造を読んでる。
計算量の解析において1回の計算に要するコストだけに注目するのではなく、アルゴリズム中で繰り返しなされる計算の平均について好ましい性能をもつかどうかを解析することをならし計算量(mortized analysis)という。つまり、単純に各ステップの計算量を積み上げるのではなく、コストの高い計算の実行される頻度を考えてアルゴリズムを決定すれば、アルゴリズムの選択肢が十分に広がってシアワセということ。
例えば最初に10の領域を確保し![]() 個の値をベクトルに格納するときを考える時、
個の値をベクトルに格納するときを考える時、![]() であれば計算量は
であれば計算量は![]() である。しかし、
である。しかし、![]() の時は、新たに10の領域を追加確保しそれまで格納した
の時は、新たに10の領域を追加確保しそれまで格納した ![]() 個の値を新しい領域にコピーしなければならない。この時全体のコピー数は
個の値を新しい領域にコピーしなければならない。この時全体のコピー数は
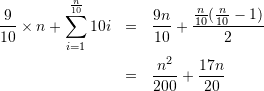
となる。これを ![]() で割ると平均で計算量は
で割ると平均で計算量は ![]() となる。ところで、新たに領域を10追加確保するのではなく「最初は1の大きさで、領域が一杯になる毎に領域の大きさを倍にする」方法では、
となる。ところで、新たに領域を10追加確保するのではなく「最初は1の大きさで、領域が一杯になる毎に領域の大きさを倍にする」方法では、
![]()
となり、これを![]() で割れば平均の計算量は
で割れば平均の計算量は![]() となる。つまり、アルゴリズムの選択肢が広がるということである。
となる。つまり、アルゴリズムの選択肢が広がるということである。
上記例はhttp://www.ieice-hbkb.org/files/06/06gun_03hen_01.pdfを参照しました。
