大学新入生のための「数学入門」第2章 関数とグラフ。グラフ電卓であっさり作図していたらなにも覚えられない。
作図のための基本型![]() に持ち込むための平方完成から。
に持ち込むための平方完成から。
平方完成
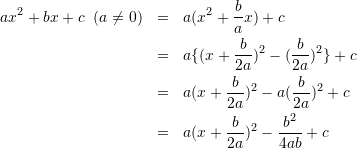
この変形で![]() として頂点が定まる。また、
として頂点が定まる。また、![]() のとき上に向かって凸、
のとき上に向かって凸、![]() の時、下に向かって凸の放物線となる。
の時、下に向かって凸の放物線となる。
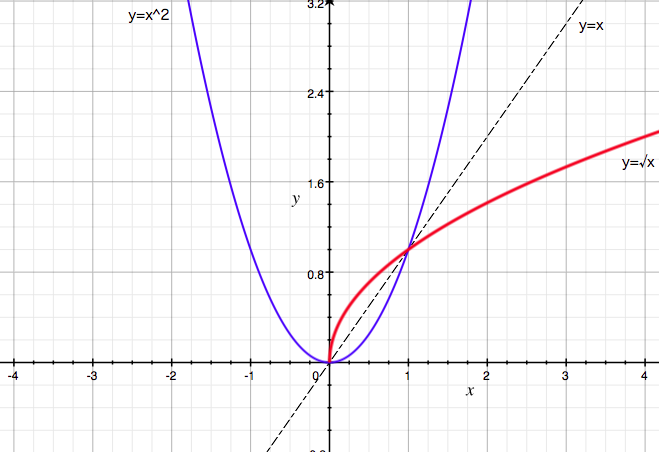
1次方程式なら直線、2次方程式なら放物線、2次方程式の放物線を![]() について対称に移すと
について対称に移すと![]() のグラフとなる。
のグラフとなる。
円の方程式
中心が原点![]() で半径
で半径![]() の円の方程式は
の円の方程式は
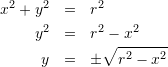
このグラフを![]() 軸方向に
軸方向に![]() 、
、![]() 軸方向に
軸方向に![]() 並行移動させると、
並行移動させると、
![]()
中心![]() 、半径
、半径![]() の円の方程式となる。
の円の方程式となる。
| 大学新入生のための数学入門 増補版 | |
 | 石村 園子 共立出版 2004-10-15 |
