大学新入生のための「数学入門」１章まとめ

Posted by

数学検定を受検しようかと思い、勉強をはじめた。大学新入生のための「数学入門」第１章　数と式の計算まで読了。ほとんど忘れているのでまとめておく。この章のキモは展開公式。

基本計算すればよいのだが方程式など解く際の因数分解など型を見抜けないと恐ろしく時間がかかったりするので右辺左辺の両方向について頭に叩き込んでおかなければ試験には厳しい。

展開公式

    \begin{eqnarray*} (a\pm b)^{2} &=& a^{2}\pm 2ab + b^{2} \\ (a\pm b)^{3} &=& a^{3}\pm 3a^{2}b + 3ab^{2} \pm b^{3}\\ (a + b)(a - b) &=& a^{2} - b^{2}\\ (x + a)(x + b) &=& x^{2} + (a + b)x + ab\\ (ax + b)(cx + d) &=& acx^{2} + (ad + bc)x + bd\\ (a + b + c)^{2} &=& a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac\\ a^{3}\pm b^{3} &=& (a\pm b)(a^{2}\mp ab + b^{2}) \end{eqnarray*}

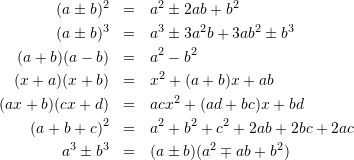
部分分数展開

    \begin{eqnarray*} \frac{1}{(x+p)(x+q)} &=& \frac{a}{x+p} + \frac{b}{x + q}\\ \frac{1}{(x + p)(x + q)^{2}} &=& \frac{a}{x + p} + \frac{b}{x + q} + \frac{c}{(x + q)^{2}}\\ \frac{1}{(x+p)(x^{2}+qx+r)} &=& \frac{a}{x + p} + \frac{bx + c}{x^{2}+qx+r} \end{eqnarray*}

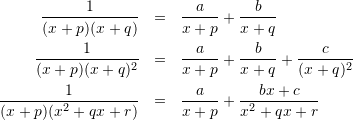
2次方程式の解の公式

    \begin{eqnarray*} ax^{2}+bx+c &=& 0\\x&=&\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\\ ax^{2}+2bx+c &=& 0\\x&=&\frac{-b\pm\sqrt{b^{2}-ac}}{a} \end{eqnarray*}

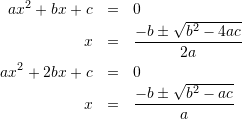
因数定理

P(a)=0なら、多項式P(x)は(x-a)で割り切れる

展開公式からはじまって代数方程式の問題では上記の公式を使い解く。式の因数分解の際、上記公式の型をすばやく見破ることができるか？制限時間のある試験の場合、それが大切。