2桁の2進数![]() を表す整数を
を表す整数を![]() とする。2進数
とする。2進数![]() が表す整数を
が表す整数を![]() の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
- ア

- イ

- ウ

- エ

2進数![]() を表す整数
を表す整数![]() は、
は、
(1) ![]()
2進数![]() を表す整数
を表す整数![]() は、(1)同様
は、(1)同様
(2) ![]()
(1)を![]() と変形して(2)に代入すると
と変形して(2)に代入すると
(3) 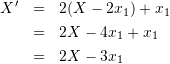
ここで、![]() を2で割った商は、
を2で割った商は、
(4) 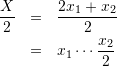
![]() となる。したがって、
となる。したがって、
(5) ![]()
(5)を(3)に代入して、![]() よって答えウ
よって答えウ
2桁の2進数![]() を表す整数を
を表す整数を![]() とする。2進数
とする。2進数![]() が表す整数を
が表す整数を![]() の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
の式で表したものはどれか。ここで、int(r)は非負の実数rの小数点以下を切り捨てた整数を表す。
2進数![]() を表す整数
を表す整数![]() は、
は、
(1) ![]()
2進数![]() を表す整数
を表す整数![]() は、(1)同様
は、(1)同様
(2) ![]()
(1)を![]() と変形して(2)に代入すると
と変形して(2)に代入すると
(3) 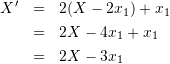
ここで、![]() を2で割った商は、
を2で割った商は、
(4) 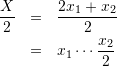
![]() となる。したがって、
となる。したがって、
(5) ![]()
(5)を(3)に代入して、![]() よって答えウ
よって答えウ
![]() である。これを踏まえて、
である。これを踏まえて、![]() を既約分数で表せ
を既約分数で表せ
![]() とおき、1000000倍して小数部を取る。
とおき、1000000倍して小数部を取る。
![]()
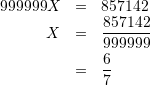
これは、解き方を知っていたのでできたのだが、約分するのに電卓使ったので反則か?解答はもっとクールだった。というか、この解法では全然「これを踏まえて」ないのでダメですね。約分も難しい(電卓使いました)し。
模範解答は、![]() としておいて、
としておいて、
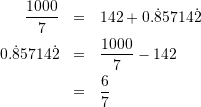
しかし、約分するときが気がついたんだけど、![]() 、面白いな。
、面白いな。
図のように長方形ABCDと正方形PQRSが辺を共有して接している。AS=12、CQ=9であるとき長方形ABCDの周の長さを求めよ。

辺![]() とおくと、
とおくと、![]() 、
、![]() であるから辺ADは
であるから辺ADは
![]()
また、![]() は正方形であるので
は正方形であるので![]() である。したがって、
である。したがって、![]() の周の長さは$
の周の長さは$

結構面白い問題でした。一応、ヒントなしで解けました。
| “数学ができる”人の思考法~数学体幹トレーニング60問~ (数学への招待) | |
 | 吉田 信夫 技術評論社 2015-10-28 |
ある規則でならぶ下記の数列
![]()
の80番目までの和を求めよ。
分母毎のグループの個数に注目すると、![]() であるので、分母が
であるので、分母が![]() の最後(
の最後(![]() )は数列の10番目(
)は数列の10番目(![]() )であることがわかる。同様に、
)であることがわかる。同様に、![]() であるから数列の78番目は
であるから数列の78番目は![]() 、79番目は
、79番目は![]() 、80番目は
、80番目は![]() である。
である。
したがって、求める数列の和は![]() である。この数列を分母毎にグループにまとめると
である。この数列を分母毎にグループにまとめると
![]()
の公差![]() の等差数列となる。したがって80番目までの和は、上記数列の12番目までの和に
の等差数列となる。したがって80番目までの和は、上記数列の12番目までの和に![]() を加えたものである。
を加えたものである。
ゆえに、80番目までの数列の和

となる。
「やさしい応用情報処理技術者講座」にややこしいのが、解りやすくまとめてあったのを写経。
数値を有効桁数にする際の誤差。例えば![]() は
は![]() として表現できるが
として表現できるが![]() は
は![]() となり循環するためこのまま表現することができない。つまり、正確に
となり循環するためこのまま表現することができない。つまり、正確に![]() をあらわすことができない
をあらわすことができない
計算を途中で打ち切ることにより生じる誤差。例えば方程式の解を求める際に計算を途中で打ち切って解の近似値を得る場合などを言う
絶対値がほぼ等しい2数を計算するとき有効数字(有効桁数)が減ってしまうことを言う。例えば、![]() は有効数字が5桁から1桁にけた落ちしている。
は有効数字が5桁から1桁にけた落ちしている。
絶対値の大きな数値と絶対値の小さな数値を演算したとき小さな値のけたの情報が落ちてしまうこと。例えば有効桁を4桁として![]() を計算するとき2つの指数の桁を揃える必要があるが、このとき小さな数値が有効桁数に収まらなくなってしまい情報落ちが発生する。(
を計算するとき2つの指数の桁を揃える必要があるが、このとき小さな数値が有効桁数に収まらなくなってしまい情報落ちが発生する。(![]() )
)
絶対値が大きいため、一定のビット数で表現できる範囲を超えてしまうこと。例えば![]() は8ビットでは表現することができない。
は8ビットでは表現することができない。
絶対値が小さいため表現できなくなること。例えば![]() は8ビット固定小数点では表現することができない。
は8ビット固定小数点では表現することができない。
| やさしい応用情報技術者講座 2016年版 (「やさしい講座」シリーズ) | |
 | 高橋 麻奈 SBクリエイティブ 2015-11-26 |
2の補数を使って加算演算する場合、
2の補数表現について、![]() ビットで表現可能な範囲は、
ビットで表現可能な範囲は、![]() 〜
〜![]() となる。例えば
となる。例えば![]() のとき
のとき![]() でOKだが、
でOKだが、![]() となってしまう。
となってしまう。
単精度(32Bit)の場合
符号(1bit) + 指数部(8bit) + 仮数部(23bit)
で表現する。
たとえば![]() は
は![]() であるから、浮動小数形式形式では符号は0、指数部は
であるから、浮動小数形式形式では符号は0、指数部は![]() 、仮数部は
、仮数部は![]() (23ビットになるようゼロを埋める)となり、つまり
(23ビットになるようゼロを埋める)となり、つまり![]() と表現される。
と表現される。
指数が有理数とはどういう意味か?これまでとりあえず「覚える」ってことでやりすごしてきたけ吉田武の「虚数の情緒」に解説。まず指数法則のおさらい、
![]()
![]()
ここで、![]() は整数であり、
は整数であり、
![]()
![]()
である。このとき![]() であるが、
であるが、![]() として考え上記指数法則を適用すると
として考え上記指数法則を適用すると
![]()
となる。このとき最後の()の中身に注目するとこれは2乗して![]() になる数つまり
になる数つまり![]() の平方根
の平方根![]() にほかならない。つまり、
にほかならない。つまり、
![]()
である。
ほんと吉田氏の本は面白い。
ある自然数![]() があるとき、
があるとき、![]() から
から ![]() までのすべての整数を合計は、
までのすべての整数を合計は、![]() である。
である。
(証明)
![]() を仮定し、
を仮定し、![]() を代入する
を代入する
![]()
両辺を展開して、
![]()
分母を揃え
![]()
左辺を整理すると
![]()
4番目についてはさらに詳しく、(ミルカさん、いや「僕」がいいそうな)
ここまでやるのは、凡人にとって「わずかな変更」ではなけどね。
 | 数学オリンピックチャンピオンの美しい解き方 テレンス・タオ 寺嶋英志 青土社 2010-07-23 |