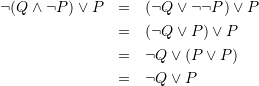数学ガールに微分と積分について良いまとめがあったのでメモ。
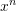 の微分
の微分
1.指数を係数に掛ける
2.指数を1減らす
![]()
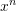 の積分
の積分
1.指数を1増やす
2.それで係数を割る
![]()
数学ガールに微分と積分について良いまとめがあったのでメモ。
1.指数を係数に掛ける
2.指数を1減らす
![]()
1.指数を1増やす
2.それで係数を割る
![]()
カシオ fx-JP900とSHARP EL-520Mのキーボード比較。10キーを除く部分でキーボード上の刻印のみです
| CASIO | SHARP | 機能 |
|---|---|---|
| shift | 2ndF | シフト |
| ALPHA | ALPHA | アルファ |
| MATH | 関数入力(キー刻印以外の関数) | |
| hyp | ハイパポリック(双曲線) | |
| sin | sin | サイン(正弦・三角関数) |
| cos | cos | コサイン(余弦) |
| tan | tan | タンジェント(正接) |
| インテグラル(積分) | ||
| 60進法(度・ディグリー、分・ミニッツ、秒・セカンド) | ||
| CNST | CNST | コンスタント(定数) |
| べき乗 | ||
| 2乗 | ||
| log | log | 常用対数 |
| ln | ln | 自然対数 |
| 逆数 | ||
| 平方根 | ||
| Exp | Exp | エクスポーネント(指数部) |
| a/b | 分数入力 | |
| RCL | リコール(メモリ呼び出し) | |
| STO | STO | ストア(メモリ記憶) |
| M+ | M+ | メモリープラス(直前の計算結果をメモリに加算) |
| CHANGE | S(Standard) D(decimal)変換 |
| No. | クライアント | サーバ |
|---|---|---|
| 1 | パラメタ開示の送信 | |
| 2 | 決定したパラメタ・サーバ乱数返信 | |
| 3 | サーバ証明書の送信 | |
| 4 | クライアント証明書の要求 | |
| 5 | メッセージの終了 | |
| 6 | クライアント証明書送信 | |
| 7 | プレマスターシークレットの生成 | |
| 8 | プレマスターシークレットをサーバ公開鍵で暗号化して送信 | |
| 9 | これまでのハンドシェイクメッセージをクライアント秘密鍵で暗号化し、デジタル署名として返信 | |
| 10 | プレマスターシークレットおよびサーバからの乱数を使用してマスターシークレットとMAC鍵を生成 | |
| 11 | マスターシークレットとここまでのメッセージを入力値として共通鍵にて検証データを生成送信 | |
| 12 | プレマスターシークレットおよびの乱数を使用してマスターシークレットとMAC鍵を生成 | |
| 13 | マスターシークレットとここまでのメッセージを入力値として共通鍵にて検証データを生成送信 |
面白かったので書籍も購入してみた。他にも![]() とか
とか![]() とか
とか![]() とかあって結構使えるんじゃないかな?
とかあって結構使えるんじゃないかな?
| インド式かんたん計算法―1冊で頭がよくなる 大人も子どもも、楽しみながら「算数脳」になる! (知的生きかた文庫) | |
 | 水野 純 ニヤンタ デシュパンデ 三笠書房 2007-08 |
11〜19の2桁九九というのを知った。インドではこうやるらしい。例えば![]() の場合。一方の数(ここでは14)に他方の一の位を足して10倍する。
の場合。一方の数(ここでは14)に他方の一の位を足して10倍する。
(1) ![]()
次に、一の位どおしをかけ算する。
(2) ![]()
これらを足して、
(3) ![]()
11から19までの数を![]() と置いて計算してみる。
と置いて計算してみる。
![]()
![]() の部分が上記(1)に当たる
の部分が上記(1)に当たる![]() の部分。
の部分。![]() がそのまま(2)の
がそのまま(2)の![]() だから、一方の数
だから、一方の数![]() に他方の一の位
に他方の一の位![]() を足して10倍した値に、両者の一の位を掛けたもの
を足して10倍した値に、両者の一の位を掛けたもの![]() を足すと答えがでる。
を足すと答えがでる。
小学生か中学生の頃覚えたかった。他にも色々あるらしいのでインド式を勉強しよう。
遅延評価のメリットを一言で
与えられた式の評価はその結果が必要になるまで遅延、停止(suspend)することである。もう1つは、停止している式が初めて評価されたとき、その結果ががメモ化(memoize)される(キャッシュされる)ことで、同じ結果が将来もう一度必要になったときに再計算せず引いてくるだけで済むことである。
「純粋関数型データ構造」
これはいいまとめだと思う。
純粋関数型データ構造を読んでる。
計算量の解析において1回の計算に要するコストだけに注目するのではなく、アルゴリズム中で繰り返しなされる計算の平均について好ましい性能をもつかどうかを解析することをならし計算量(mortized analysis)という。つまり、単純に各ステップの計算量を積み上げるのではなく、コストの高い計算の実行される頻度を考えてアルゴリズムを決定すれば、アルゴリズムの選択肢が十分に広がってシアワセということ。
例えば最初に10の領域を確保し![]() 個の値をベクトルに格納するときを考える時、
個の値をベクトルに格納するときを考える時、![]() であれば計算量は
であれば計算量は![]() である。しかし、
である。しかし、![]() の時は、新たに10の領域を追加確保しそれまで格納した
の時は、新たに10の領域を追加確保しそれまで格納した ![]() 個の値を新しい領域にコピーしなければならない。この時全体のコピー数は
個の値を新しい領域にコピーしなければならない。この時全体のコピー数は
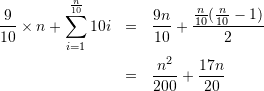
となる。これを ![]() で割ると平均で計算量は
で割ると平均で計算量は ![]() となる。ところで、新たに領域を10追加確保するのではなく「最初は1の大きさで、領域が一杯になる毎に領域の大きさを倍にする」方法では、
となる。ところで、新たに領域を10追加確保するのではなく「最初は1の大きさで、領域が一杯になる毎に領域の大きさを倍にする」方法では、
![]()
となり、これを![]() で割れば平均の計算量は
で割れば平均の計算量は![]() となる。つまり、アルゴリズムの選択肢が広がるということである。
となる。つまり、アルゴリズムの選択肢が広がるということである。
上記例はhttp://www.ieice-hbkb.org/files/06/06gun_03hen_01.pdfを参照しました。
集合族(元がすべて集合である集合:集合の集合)
![]() がすべて集合
がすべて集合![]() の部分集合であるとき、それらを集めてできる集合
の部分集合であるとき、それらを集めてできる集合![]() も集合族である。
も集合族である。
つまり、![]() と
と![]() は、それぞれ
は、それぞれ![]() および
および![]() と同義である。例えば、
と同義である。例えば、
![]() のとき
のとき![]() 、
、![]() となる。
となる。
数検4級で面白い問題。「分数のわり算はひっくり返して掛ける」と機械的に覚えさせられている小学生に良い問題だと思う。
14÷2と28÷4のように、わり算では、わられる数とわる数に同じ数をかけても、商は変わりません。このことを利用して、よしゆきさんは「分数のわり算はわる数の逆数をかけて求めることができる」ことを次の式から考えました。
![]()
(1) ![]() 、
、![]() 、
、![]() 、
、![]() のうち
のうち![]() 、
、![]() に当てはまるものはどれですか。
に当てはまるものはどれですか。
(2) この式の続きを計算し、よしゆきさんの考えを言葉で書きなさい。
同じ数をかけるのだから、![]() に
に![]() をかけるのであれば、
をかけるのであれば、![]() にも
にも![]() かける必要があるので答えは
かける必要があるので答えは![]()
![]()
計算結果は下記のとおり。
わる数とわられる数の双方にわる数の逆数をかけることと、わられる数にわる数の逆数をかけることと同じである。
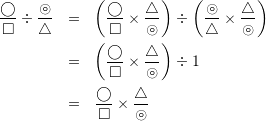
今更だけど基礎。(その理屈、証明できますか?より)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
状況に応じて複雑な式を変形できることが大事。