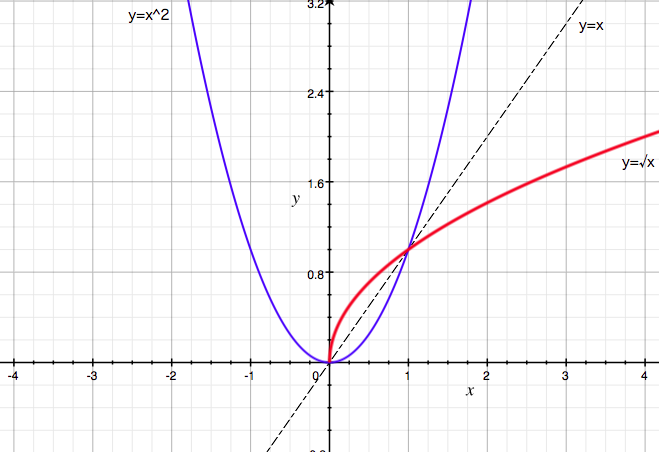
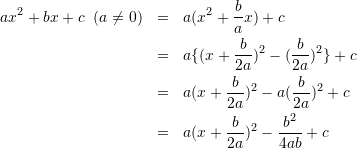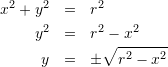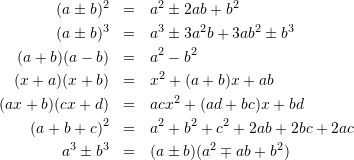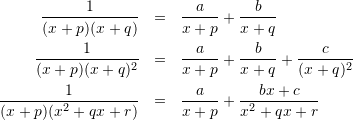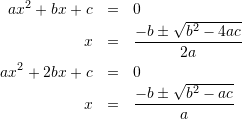美意識

Posted 2018-07-07 by kztkym

けっきょくのところその際の基準は、美的なものでなくてはならない。数学にはこのほかにも、深みとか一般性とか有用性とかいった価値がある。しかしこれらは、それ自体としてはさしたる目標にならない。これらの価値の意義は、関連するほかのものの価値によって変わる。数学における究極の価値は、ただ美的であること。つまり、音楽や絵画といった芸術形態に見いだされる美的な価値なのだ。

ロジャー・ペンローズ（ 1931- 英国の数学者）

あぁ、カッコいいな。今読んでいる「１から学ぶ大人の数学教室」で紹介されている言葉。数学とかプログラミングに、これらの小片を発見したからこそ惹かれるんだろうな。数学やプログラミングが好きで良かった。

情報処理安全確保支援士試験合格！

Posted 2018-07-06 by kztkym

情報処理安全確保支援士試験、試験後の手応えは前回のほうが良かったのだがなんとか引っかかって合格。特に午後Ⅱはほんとギリギリ。これまでの試験でも1点、2点に泣いてきたけど今度は62点で笑った。午後Ⅰは予想を上回って高得点だったのが自分でも予想外。

問題の登録だけど交渉の結果、登録にかかる諸費用およびEラーニングと集合研修の費用等は会社持ちなった。これでハレて登録セキュリティスペシャリストってことになる。惜しむらくは、資格手当がつくともっと良かったのになぁ。たぶん、あいつの差し金（などと考えるところに心の貧しさがある）。

あと一度分午前免除の権利があるけど「ネットワークスペシャリスト」受けようか思案中。なんとなく勉強する気分ではなくなってしまっているしなぁ。

IPアドレスの計算法

Posted 2017-10-21 by kztkym

情報処理関係の本は色々と読んでいるとは思うのだが、この方法は初めて知った。減算だけでいいのでかなり楽ちん。

$2^{0}$ から $2^{7}$ までを10進数に変換した表を作成し左から大きい順にならべた表を作成する。例として「172を二進変換」する手順を考える。

まず変換対称の $172$ から減算して正の数となる数を表の右端から順に探す。 $172-128>0$ なのでその計算をする。結果は $44$ 。この時 $128$ のマスに $1$ を立てる。
次に(1)の計算結果 $44$ から減算して正の数となる数を右端から順に探す。 $44-32>0$ なのでその計算をする。結果は $12$ 。(1)と同様 $32$ のマスに $1$ を立てる。また、減算できずスキップした $64$ のマスには $0$ を立てる。
上記を繰り返す

$2^{7}$	$2^{6}$	$2^{5}$	$2^{4}$	$2^{3}$	$2^{2}$	$2^{1}$	$2^{0}$
128	64	32	16	8	4	2	1
1	0	1	0	1	1	0	0
$44$	–	$12$	–	$4$	$0$	–	–

ネットワークスペシャリスト教本より

この計算尺は使えると思いますよ

大学新入生のための「数学入門」第4章まとめ

Posted 2017-10-18 by kztkym

大学新入生のための「数学入門」第4章　指数関数。根と指数はなんとなく苦手感がある。法則を押さえ、練習あるのみなのだが…

指数法則

$\begin{eqnarray*} a^{\frac{m}{n}}&=&\sqrt[n]{a^{m}}\\ \frac{1}{a^{n}}&=& a^{-1}\\ a^{p}\cdot a^{q}&=& a^{p+q}\\ (a^{p})^{q} &=& a^{pq}\\ (a\cdot b)^{p}&=& a^{p}\cdot b^{p}\\ \frac{a^{p}}{a^{q}}&=&a^{p-q}\\ (\frac{a}{b})^{p}&=&\frac{a^{p}}{b^{p}} \end{eqnarray*}$

例題

$\begin{eqnarray} \frac{\sqrt[4]{2}\times \sqrt[8]{8}}{\sqrt{2}}&=&\frac{2^{\frac{1}{4}}\times 8^{\frac{1}{8}}}{2^{\frac{1}{2}}}\\ &=&2^{\frac{1}{4}}\cdot (2^{3})^{\frac{1}{8}}\cdot 2^{-\frac{1}{2}}\\ &=&2^{\frac{1}{4}}\cdot 2^{\frac{3}{8}}\cdot 2^{-\frac{1}{2}}\\ &=&2^{\frac{1}{4}+\frac{3}{8}-\frac{1}{2}}\\ &=&2^{\frac{1}{8}}\\ &=&\sqrt[8]{2} \end{eqnarray}$

アタマのいい人

Posted 2017-10-14 by kztkym

まして今まで慣れ親しんできた角度の「度」という単位をなぜ捨てて、ラジアンなどという新しい角度の単位を考え出さなければならないのかわかりませんでした。（中略）また、「 $2^{\frac{3}{2}}$ 」とはどういう数なのか、なぜそんな数を考えなければならないのか、その意味がさっぱりわかりませんでした。まして「 $2^{\sqrt{3}}$ 」などという数が本当にあるのか。どうしてそんな数を考えなければならないのか、その必然性もつかめませんでした。

数学の教科書が言ったこと、言わなかったこと（南みや子）

あ〜、これ分かるは。これが、スッと理解できる人がアタマのいい人、ココを飛ばしてとりあえず問題に向き合える人が成績のいい人。という印象。これを解消してくれる良い先生が近くにいた人が幸運な人。

数学の教科書が言ったこと、言わなかったこと (BERET SCIENCE)
	南みや子ベレ出版 2014-04-22 売り上げランキング : 304218 Amazonで詳しく見る by G-Tools

大学新入生のための「数学入門」２章まとめ

Posted 2017-09-22 by kztkym

大学新入生のための「数学入門」第２章　関数とグラフ。グラフ電卓であっさり作図していたらなにも覚えられない。

作図のための基本型 $y=a(x-p)^{2}+q$ に持ち込むための平方完成から。

平方完成

$\begin{eqnarray*} ax^{2}+bx+c\;\;(a\neq 0) &=& a(x^{2}+\frac{b}{a}x)+c\\ &=& a\{(x+\frac{b}{2a})^{2}-(\frac{b}{2a})^{2}\}+c\\ &=& a(x+\frac{b}{2a})^{2}-a(\frac{b}{2a})^{2}+c\\ &=& a(x+\frac{b}{2a})^2-\frac{b^{2}}{4ab}+c \end{eqnarray*}$

この変形で $(p,q) = (\frac{b}{2a},-a(\frac{b}{2a})^{2}+c)$ として頂点が定まる。また、 $a<0$ のとき上に向かって凸、 $a>0$ の時、下に向かって凸の放物線となる。

1次方程式なら直線、2次方程式なら放物線、2次方程式の放物線を $y = x$ について対称に移すと $y = \pm\sqrt{x}$ のグラフとなる。

円の方程式

中心が原点 $O(0,0)$ で半径 $r$ の円の方程式は

$\begin{eqnarray*} x^{2}+y^{2} &=& r^{2}\\ y^{2} &=& r^{2} - x^{2}\\ y &=& \pm\sqrt{r^{2}-x^{2}} \end{eqnarray*}$

このグラフを $x$ 軸方向に $p$ 、 $y$ 軸方向に $q$ 並行移動させると、

$\begin{eqnarray*} (x-p)^{2} + (y-q)^{2}=r^{2} \end{eqnarray*}$

中心 $(p,q)$ 、半径 $r$ の円の方程式となる。

大学新入生のための数学入門増補版
	石村園子共立出版 2004-10-15 売り上げランキング : 44635 Amazonで詳しく見る by G-Tools

大学新入生のための「数学入門」１章まとめ

Posted 2017-09-21 by kztkym

数学検定を受検しようかと思い、勉強をはじめた。大学新入生のための「数学入門」第１章　数と式の計算まで読了。ほとんど忘れているのでまとめておく。この章のキモは展開公式。

基本計算すればよいのだが方程式など解く際の因数分解など型を見抜けないと恐ろしく時間がかかったりするので右辺左辺の両方向について頭に叩き込んでおかなければ試験には厳しい。

展開公式

$\begin{eqnarray*} (a\pm b)^{2} &=& a^{2}\pm 2ab + b^{2} \\ (a\pm b)^{3} &=& a^{3}\pm 3a^{2}b + 3ab^{2} \pm b^{3}\\ (a + b)(a - b) &=& a^{2} - b^{2}\\ (x + a)(x + b) &=& x^{2} + (a + b)x + ab\\ (ax + b)(cx + d) &=& acx^{2} + (ad + bc)x + bd\\ (a + b + c)^{2} &=& a^{2} + b^{2} + c^{2} + 2ab + 2bc + 2ac\\ a^{3}\pm b^{3} &=& (a\pm b)(a^{2}\mp ab + b^{2}) \end{eqnarray*}$

部分分数展開

$\begin{eqnarray*} \frac{1}{(x+p)(x+q)} &=& \frac{a}{x+p} + \frac{b}{x + q}\\ \frac{1}{(x + p)(x + q)^{2}} &=& \frac{a}{x + p} + \frac{b}{x + q} + \frac{c}{(x + q)^{2}}\\ \frac{1}{(x+p)(x^{2}+qx+r)} &=& \frac{a}{x + p} + \frac{bx + c}{x^{2}+qx+r} \end{eqnarray*}$

2次方程式の解の公式

$\begin{eqnarray*} ax^{2}+bx+c &=& 0\\x&=&\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\\ ax^{2}+2bx+c &=& 0\\x&=&\frac{-b\pm\sqrt{b^{2}-ac}}{a} \end{eqnarray*}$

因数定理

$P(a)=0$ なら、多項式 $P(x)$ は $(x-a)$ で割り切れる

展開公式からはじまって代数方程式の問題では上記の公式を使い解く。式の因数分解の際、上記公式の型をすばやく見破ることができるか？制限時間のある試験の場合、それが大切。

TI-83 Plusベンチ

Posted 2017-09-13 by kztkym

[電卓喫茶]測定して気がついたこと2にあったベンチをTI-83 Plusでもやってみた。

お題は

$\begin{eqnarray*} \sum_{x=0}^{10^2}x(sin(x)+cos(x)+1) \end{eqnarray*}$

TI-83 Plusは数式入力ではないので考え方としてはリストを作成してからそのリストを合計するという形式。リスト作成は[2nd]-[STAT]から[OPS]-[5.Seq]、リストの合計は[2nd]-[STAT]から[MATH]-[5.Sum]で入力。

sum(seq(X*(sin(X)+cos(X)+1),X,0,10^2))

しばし待つこと約７秒で4941.829141でした。同じことを手持ちの他の電卓でもやった結果

CASIO fx-JP900: 約7秒
CASIO fx-912ES: 約35秒
SHARP EL-520M: 約21秒

でした。JP900とTI-83 Plusはほぼ互角の勝負ですがやはり入力は数式入力のほうが楽ですが、haskellの

sum $ map(\x->(x*(sin x + cos x + 1)))[0..10^2]

とほぼ同じだし、なんかコンピュータっぽくてむしろ好ましい…（ちなみにHaskellでは1秒かかりませんでした）また、電脳喫茶では $10^{3}$ , $10^{4}$ , $10^{5}$ まで計測していますがTI-83 Plusでは $10^{3}$ のところでERR:INVALID DIMで終了しました。

TI-83 Plus

Posted 2017-08-23 by kztkym

「6」と「ー」キーのひっかかりと、暖まっていないときの表示ちょっとおかしいのが玉に瑕だけど程度はまぁまぁです。

TI-83 Plus

x^nの微分・積分

Posted 2017-08-21 by kztkym

数学ガールに微分と積分について良いまとめがあったのでメモ。

$x^{n}$ の微分

1.指数を係数に掛ける
2.指数を1減らす

$\begin{eqnarray*} (x^{n})' \,=\, nx^{n-1} \end{eqnarray*}$

$x^{n}$ の積分

1.指数を1増やす
2.それで係数を割る

$\begin{eqnarray*} \int x^{n} dx\,=\,\frac{1}{n+1}x^{n}+C \end{eqnarray*}$

美意識

情報処理安全確保支援士試験合格！

IPアドレスの計算法

大学新入生のための「数学入門」第4章まとめ

指数法則

例題

アタマのいい人

大学新入生のための「数学入門」２章まとめ

平方完成

円の方程式

大学新入生のための「数学入門」１章まとめ

展開公式

部分分数展開

2次方程式の解の公式

因数定理

TI-83 Plusベンチ

TI-83 Plus

x^nの微分・積分

$x^{n}$ の微分

$x^{n}$ の積分

最近の投稿

アーカイブ

カテゴリー

指数法則

例題

平方完成

円の方程式

展開公式

部分分数展開

2次方程式の解の公式

因数定理

の微分

の積分

最近の投稿

アーカイブ

カテゴリー

タグ

$x^{n}$ の微分

$x^{n}$ の積分