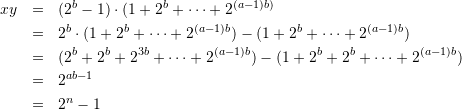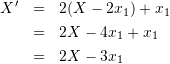論理式の基本

Posted 2017-04-19 by kztkym

今更だけど基礎。（その理屈、証明できますか？より）

ド・モルガンの法則

$\lnot(P\wedgeQ)=\lnot P \vee \lnot Q$
$\lnot(P\vee Q)=\lnot P \wedge \lnot Q$

交換法則

$P\wedge Q = Q\wedge P$
$P\vee Q=Q\vee P$

結合則

$P\wedge (Q\wedge R) = (P\wedge Q)\wedge R$
$P\vee (Q\vee R) = (P\vee Q)\vee R$

冪等則

$P\wedge P = P$
$P\vee P = P$

分配則

$P\wedge (Q\vee R) = (P\wedge Q)\vee (P\wedge R)$
$P\vee (Q\wedge R) = (P\vee Q)\wedge (P\vee R)$

吸収則

$P\vee (P\wedge Q) = P$
$P\wedge (P\vee Q) = P$

二重否定の法則

$\lnot\lnot P=P$

状況に応じて複雑な式を変形できることが大事。

$\begin{eqnarray*} \lnot(Q　\wedge \lnot　P)\vee P&=&(\lnot Q \vee\lnot\lnot P)\vee P \\ &=& (\lnot Q　\vee P)\vee P \\ &=& \lnot Q　\vee (P\vee P) \\ &=& \lnot Q　\vee P \end{eqnarray*}$

情報処理安全確保支援士試験撃沈す

Posted 2017-04-17 by kztkym

情報処理安全確保支援士試験終わりー。午前1は $\frac{24}{30}$ 、午後2は $\frac{22}{25}$ でめでたく合格圏内なんだけど、おそらく午後で撃沈。過去問に挑戦した感じではギリギリ70%はとれるかな？という感触だったがいざ本番となったらまったく手がつかず..という状態。今秋を目指します。

午後対策はほぼ過去問だけだったため、明らかに知識不足。もう少し現場に寄り添った勉強をしないとダメ。実際に体験できれば一番だけどそれは難しいので、世の中にどんなインシデントがあるのか？実際に行われた攻撃手法とか、試験過去問ばかりではなくもう少し広く事例を研究する必要があると感じた。

あとは時間配分をもう少し考えないと。とくに午後Ⅰは問題選択のための時間も考えると１問あたり40分程度。頭を切り換える必要もあるしすばやく内容を把握し解答できる力がないと。僕にとっては午後Ⅰのほうが午後Ⅱの2時間で1問のよりきつく感じる。いずれにしても根本からやり直しが必要だ。

その理屈、証明できますか

Posted 2017-04-11 by kztkym

その理屈、証明できますか

予想2 $n$ が1より大きな整数で、かつ $n$ が素数でなければ $2^{n}-1$ は素数でない

$n$ は素数ではないので、 $a < n,b < n$ かつ $n = ab$ となる２つの正の整数 $a,b$ が存在する。 $x=2^{b}-1,y=1+2^{b}+2^{2b}+\cdots+2^{(a-1)b}$ とする。そのとき次のとおり。

$\begin{eqnarray*} xy&=&(2^{b}-1)\cdot(1+2^{b}+\cdots+2^{(a-1)b) \\ &=& 2^{b}\cdot(1+2^{b}+\cdots+2^{(a-1)b}) - (1+2^{b}+\cdots+2^{(a-1)b}) \\ &=& (2^{b}+2^{b}+2^{3b}+\cdots+2^{(a-1)b}) - (1+2^{b}+2^{b}+\cdots+2^{(a-1)b}) \\ &=& 2^{ab-1} \\ &=& 2^{n}-1 \end{eqnarray*}$

下の展開式はいいとしても、そもそも $y=\cdots$ の式の立て方というか突如出現したかに見えるこの式の存在。これが僕のような凡人には理解できないところ。この式がなぜ・どういう思考回路を経て出現したのか？そこがわからないと「証明は難しい」のまま終わってしまう。そのあたりは後々の章であきらかになるのかな？とりあえず、期待して読み進む。

ステートフルインスペクション

Posted 2017-04-02 by kztkym

ダイナミックなパケットフィルタリングの一種。
レイヤ3のIPパケットが、どのレイヤ4（TCP/UDP）セッションに属するものであるか判断して、正当な手順のTCP/UDPセッションによるものとは判断できないような不正なパケットを拒否する。そのため、TCP/UDPセッションの一部情報を記憶して判断動作する。具体例として、ヘッダのSYNやACKフラグのハンドシェイクの状態などを記憶し、不正に送られてきSYN/ACKパケットを廃棄する。

ファイアウォール – Wikipedia

要するにパケット単体だけでなくその前後関係をキチン記録してパケットの通過・破棄を判断してくれるってことでよいかな。注意点としては安易な設定は運用上の負担となることとネットワーク上の負荷となり遅延などを引き起こしかねないという点

森田真生か岡潔ばっかり読んでる

Posted 2017-03-17 by kztkym

このところ、森田真生か岡潔ばっかり読んでる。

数学を勉強していると、それまでわからなかったはずのことがある瞬間にふとわかる経験をすることがある。それは、数学を学ぶ最大の喜びの瞬間でもある。

みんなのミシマガジン×森田真生０号

僕は、数学ではこの経験を残念ながらしたことがないが、プログラミングでならある。悩み続けたバグの原因はあるとき突然に「わかる」のだ。どう実装していいのか、途方に暮れていても、あるときふと「こうすればいいんじゃないか」と閃くことがある。

革新的なアプリケーションを開発しているわけじゃない。そこにある、解決すべき問題を自らのアタマで紡ぎ出したやり方で突破した喜び。数学ときっと似ているんじゃないかと思う。

リバースブルートフォース攻撃

Posted 2017-03-15 by kztkym

パスワードを固定しIDを次々に変更して侵入を試みる攻撃。

こんなのもあるんだ。パスワードブルートフォース攻撃に対しアカウントロックが防御の基本だけれど、リバースブルートフォースだとこういう防御も意味を為しにくいらしい。

中学受験

Posted 2017-03-01 by kztkym

息子の中学受験が「不合格」で終わりを遂げました。約1年の間手取足取り褒めたり叱ったり煽てたり。いろいろしましたが、結局は叶いませんでした。

すべてを遣り終えた今、後悔がないかと問われれば「もう少し早く始めれば良かった」「もっと厳しくすべきだった」とか「もっとうまく説明できたはず」とかたくさんあります。それでも、高校受験や大学受験では絶対にあり得ない（いや、あっては困る）父子二人がどっぷりと向き合って学んだこの経験は大きな塊となって僕らの記憶に残るだろうというこの一点において後悔はまったくありません。

それにしても中学受験ってなんだろう？多額のお金をかけ学校では習うことのない問題を解くことを強いる日々。地頭がよい子だけが合格するとしか思えない問題の数々。この経験から彼が何を学んだのかはうかがい知れませんが、解けなかった問題が解けるようになった時の喜び、あの感じ。ほんの少しでもそんな境地に近づいてくれたらそれで十分ではないかと思います。

岡潔（数学を志す人に）

Posted 2017-02-19 by kztkym

「数学する身体」（森田真生）がとても面白かったので、また岡潔を読み直したりしてる。岡潔の世界に少しでも近づきたい一心だ。

私たちが純一無雑に努力した結果、心情によく澄んだ一瞬ができ、時を同じくしてそこに智力の光が射したのです。そしてこの智力が数学上の発見に結びつくものなのです。

「直感力を高める数学脳のつくりかた」という本では「集中モード」「拡散モード」のように表現している。卑近な例で言えば、プログラミング時どうしてもわからないバグに悩みに悩んだあげく、例えば食事中にあるいは運転中に「すべてがわかる」心がよく澄んだあの瞬間。岡潔の言う、「調和」とはもっと大きなものかも知れないが、「集中」と「拡散」の調和が大切なのだろう。

ある形式にもたれかかって初めて自分というものがあるような気がする。これを夜の闇というのだ。（中略）しかし、数学の本体は「信」というようなものである。学ぶものが「これで間違いない」と確信して得てはじめて一歩一歩進むことができるのである。

数学の属性の第一はいつの時代になっても「確かさ」なのだから、君の出した結果は確かかと聞かれた時、確かなら確か、そうでなければそうでないとはっきり答えられるようにしておいてほしいということである。でないとあとの教えようがない。この確かさに信頼して初めて前へ進めるのだから。

情緒がなっとくするまで考え抜くこと。これが大事なのだろう。

数学する身体

Posted 2017-02-18 by kztkym

今年はまだ２ヶ月しか経っていないけれど、ここまでのナンバーワン。数学の生い立ち、古代ギリシャからアジア、そして西欧数学へと巡る旅。その過程で筆者が見、そして辿り着いた岡潔の「情緒」。これまで理解できなかったこの「情緒」が本書を読んで、少しだけわかるような気になった。本書で説かれるような、あるいは岡潔の言う「わかった」の境地にはむろんまだまだ遠いが、少なくともその地にたった気がするだけで本書を手にとって良かったと言える。

いかなる難問（パズル）を前にしても、常に「解ける」方に賭けて挑み続けたことだけは確かだ。不安の中に、すなわち間違う可能性（、、、、、、）の中にこそ「心」があると、彼は誰よりも深く知り抜いていたからである。

P110

人はみな、「風景」の中を生きている。それは、客観的な環境世界についての正確な視覚像ではなくて、進化を通して獲得された知覚と行為の連関をベース、知識や想像力と言った「主体にしかアクセスできない」要素が混入（、、）しながら立ち上げる実感である。何を知っているか、どのような世界を理解しているか、あるいは何を想像しているかが、風景の現れ方を左右する。（中略）数学者とは、この風景の虜になってしまった人のことをいう。

P125-P126